LeetCode-11 盛最多水的容器

发表于 | 分类于 | 评论数： | 阅读次数：

题目：盛最多水的容器

给定 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

img

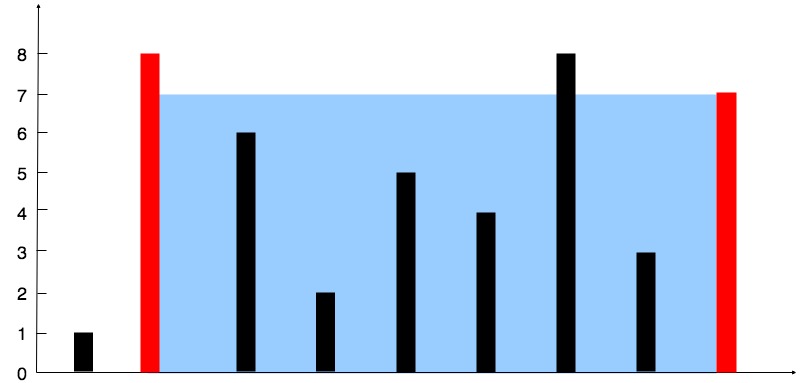
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例:

1
2
输入: [1,8,6,2,5,4,8,3,7]
输出: 49

思路

这个其实就是在数组height中找到两值，height[i]和height[j]使min(height[i], height[j]) * (j-i)最大。

直接最简单方法，经过两次遍历即可：

  • 第一个点i，从第1个数到倒数第二个数
  • 第二个点j，从第i+1个数到最后一个数
  • 计算每次的面积，保留最大面积即可

实现：

1
2
3
4
5
6
7
8
9
class Solution:
    def maxArea(self, height: List[int]) -> int:
        length = len(height)
        area = 0
        for i in range(0, length - 1):
            for j in range(i + 1, length):
                temp_area = min(height[i], height[j]) * (j - i)
                area = max(temp_area, area)
        return area

优化方法

上面的方法会有两层循环，那么怎么做到一层循环呢？

需要通过比较的方式来遍历。

  • 取第一个数i，和最后一个数j最后初始的两个数。此时围成面积的长(j-i)最大。
  • 后续只可能缩短长(j-i)，但这时必须时高更大才可能比之前的面积大，所以是移动i，j两个位置中数值较小的那个
    • height[i]<height[j]，把i往后移动：i++
    • height[i]>height[j]，把j往前移动：j–
  • 直到i=j这时循环结束，返回最大值

实现：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def maxArea(self, height: List[int]) -> int:
        area = 0
        l = 0
        r = len(height) - 1
        while r > l:
            area = max(area, min(height[l], height[r]) * (r - l))
            if height[l] > height[r]:
                r -= 1
            else:
                l += 1
        return area

如果大家有更好的方法，欢迎一起探讨。