该系列为南京大学课程《用Python玩转数据》学习笔记,主要以思维导图的记录
6.5 数据存取
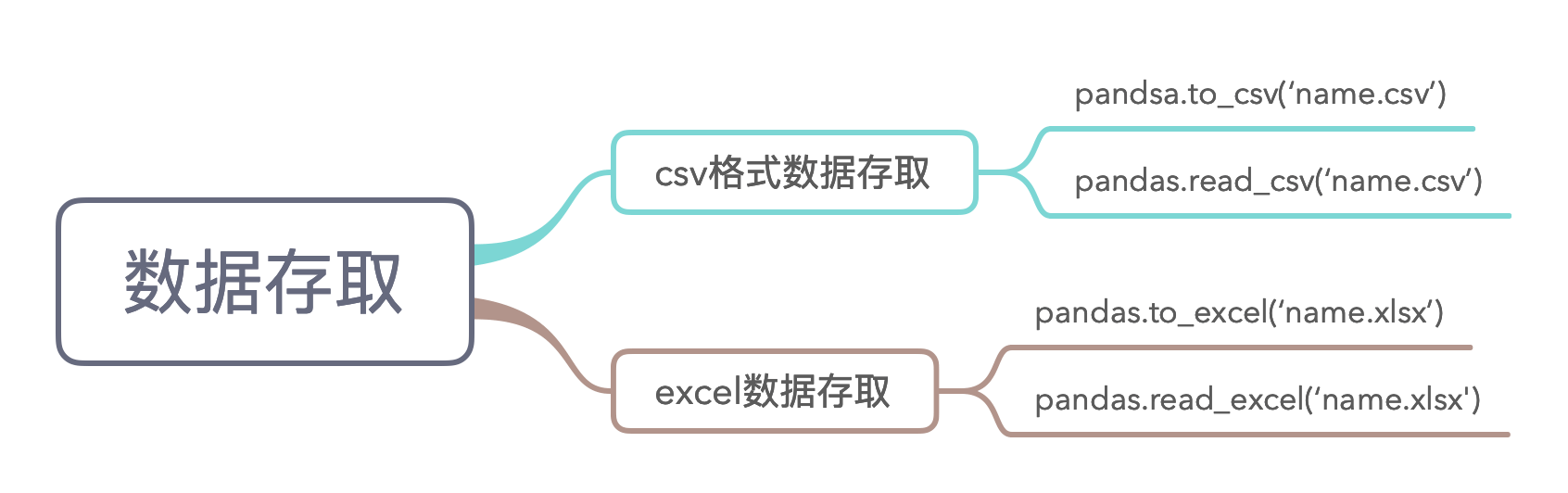
扩展:箱型图分析成绩数据
把以下数据复制到 excel 工作表中(文件名为 score.xlsx):
| Maths | English | Python | Music | Physics | Chemistry | PE | |
|---|---|---|---|---|---|---|---|
| Wang | 88 | 64 | 96 | 85 | 90 | 81 | 95 |
| Ma | 92 | 99 | 95 | 94 | 92 | 94 | 90 |
| Liu | 91 | 87 | 99 | 95 | 95 | 92 | 70 |
| Qian | 78 | 99 | 75 | 81 | 83 | 88 | 92 |
| Meng | 88 | 78 | 98 | 84 | 70 | 95 | 98 |
| Song | 100 | 95 | 100 | 92 | 98 | 95 | 65 |
利用 pandas 的 read_excel()方法读出数据保存到一个 DataFrame 中,并绘制相应的箱形图。
实现:
1 | # -*- coding: utf-8 -*- |
图像显示:
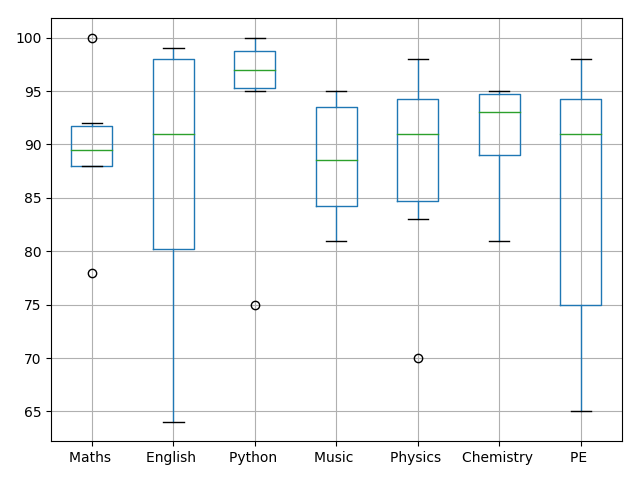
(1)哪些课程的成绩分布比较集中,哪些比较分散?你是通过什么来观察到的?
Maths、Python 和 Chemistry 分布比较集中,而 English 和 PE 的分布则比较分散,从箱子的长度可以获得这些信息;
(2)哪些课程的成绩分布比较平均(对称)?你是通过什么来观察到的?
在 7 门课程中,Python 的成绩分布最为均匀,PE 的成绩分布最不均匀,从中位数到上四分位和下四分位的距离比较可以获得这些信息;
(3)哪些课程的成绩总体较好?哪些总体较差?你是通过什么来观察到的?
Python 的总体情况最好,Maths、English 和 Music 的总体情况不太理想,从中位数的位置可以获得这些信息,分析数据可以发现这 3 门课程中各有 3 个同学没有达到 90 分,PE 虽然从图中看平均值应该不高,但其总体情况较好,分析数据可以发现有 2 个同学考了低分但 90 以上的有 4 个同学;
(4)哪些课程的成绩存在与总体情况不相符的值?你是通过什么来观察到的?
Maths、Python 和 Physics 中分别有 2 个、1 个、1 个异常值(离群点),箱形图中会将这些异常值单独列出,一是为了一目了然地表明数据中的异常,二是为了不因为这些少数的异常数据导致整体特征的偏移。
6.6 Python的理工类应用
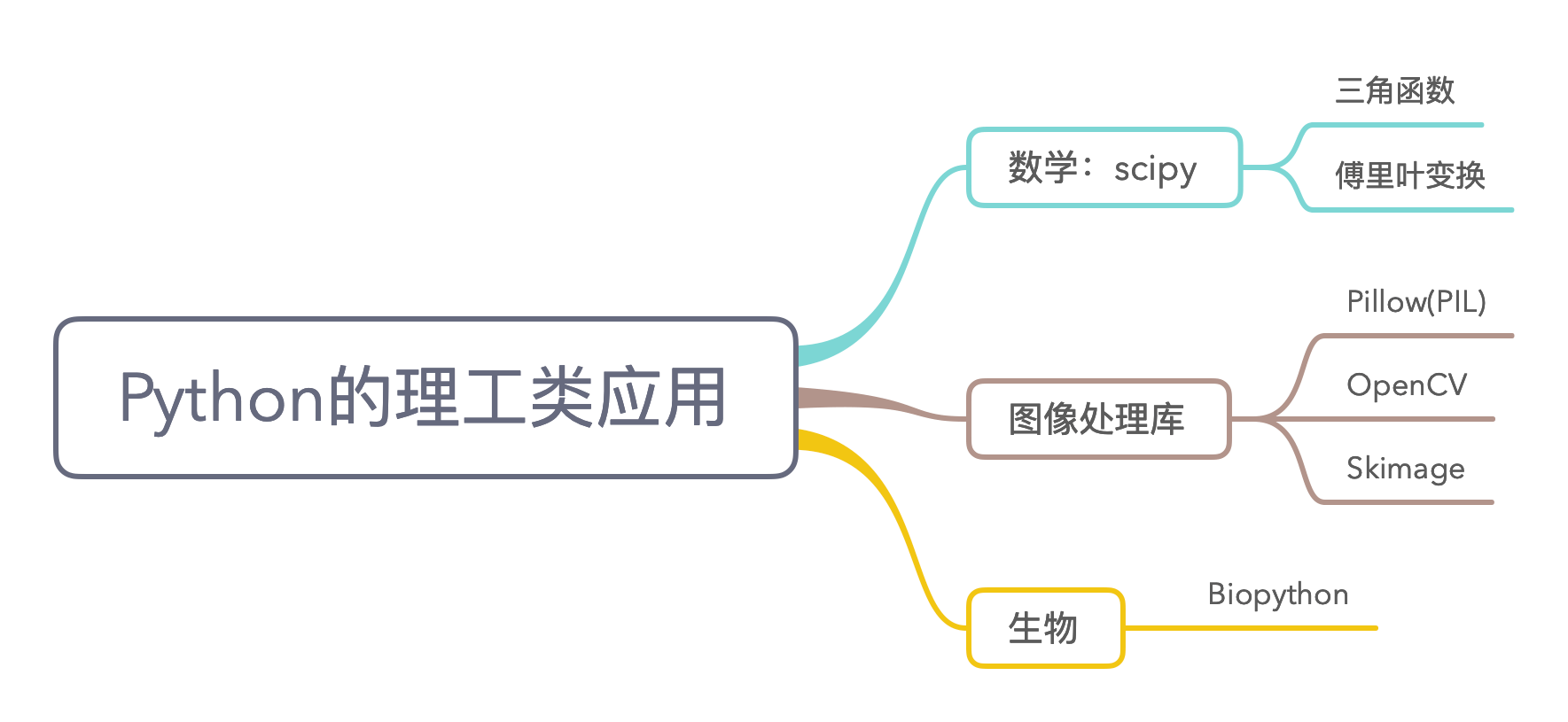
扩展:WAV音频处理入门研究
1. 网络数据读取与保存
主要使用 urllib.request 模块此处选择位于 http://www.nch.com.au/acm/11k16bitpcm.wav 的音频作为数据源,使用 urllib.request.urlopen()函数取得该文件,并以‘english.wav’的文件名保存在本地的程序所在路径。
实现:
1 | # 获取wav文件 |
2. 简单幅度处理
使用 wavfile 模块可以比较简单地从 wav 格式的文件中读取出相应的采样率、数据等信息,而不必关心文件的格式细节。python 的 wave 模块也有相应的操作,示例详见代码。读取后使用 pyplot 模块,可以绘制出音频文件的波形图。
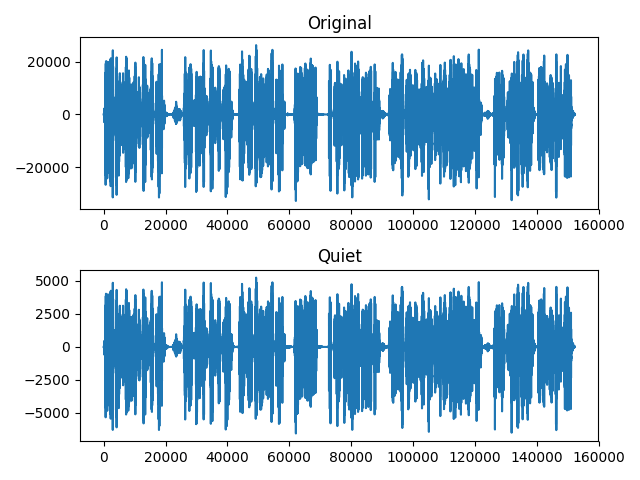
将信号幅值按比例减小,表现出来的效果就是声音强度减小。使用 numpy 模块,将原始数据与常数相乘,得到一个值减小的新数组。这里利用了 numpy的广播机制,如果两个相乘的对象长度不等,numpy 会根据一定的规则将对象扩展为相同的类型,再做运算。
计算完成后,使用 wavfile.write()函数将修改后的音频信号写入一个新的文件中,命名为’silent.wav’,采样率未修改,与原音频相同。
最后使用 matplotlib.pyplot 绘制波形图对比。
1 | # 读取wav文件 |
图像显示:
3. 简单时频分析
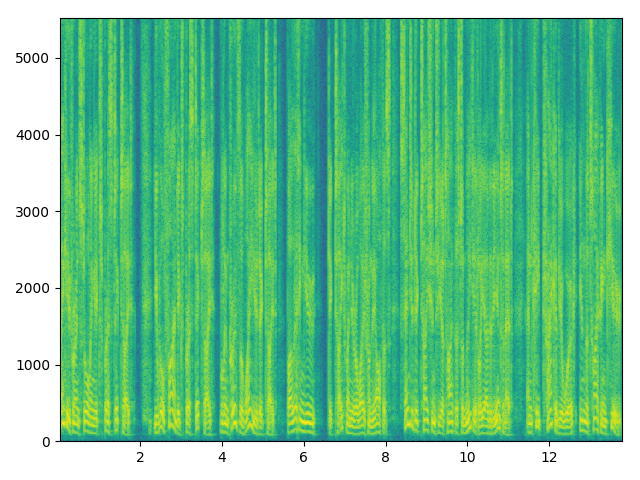
音频信号是一种常见的非平稳信号,频域特性随时间变化。时频图是分析音频信号的常用工具,在一幅图中表示出信号的频率、幅度随时间的变化。pylab 模块提供了 specgram 函数,可以简单地通过配置相应参数进行短时傅里叶变换,并输出时频图。
实现:
1 | result = matplotlib.pylab.specgram(newdata, NFFT=1024, Fs=sample_rate, noverlap=900) |
图像显示:
6.7 Python的人文社科类应用

